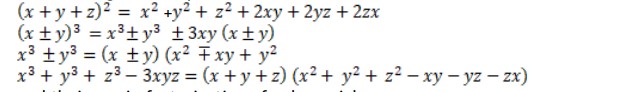CBSE Class 9 Maths Syllabus 2024-25

CBSE Class 9 Maths Syllabus 2025-26, Check Important Topics, Download PDF

by

In the Class 9 Curriculum, Mathematics is one of the most crucial subjects among all. To do well in the maths exam, you need to master all the concepts mentioned in the official CBSE Class 9 Maths Syllabus 2025-26.

Understanding the CBSE Class 9 Mathematics Syllabus 2025-26 enables students to create academic goals and arrange their studies properly in order to accomplish them. Read the full blog to know about the CBSE Class 9 Maths Topics, Marks distribution and so on.

CBSE Class 9 Maths Syllabus 2025-26

Mathematics is such a subject that matters for grades for students in Class 9 Standard. To achieve high scores in the Class 9 Maths exam, you need to grasp the concepts efficiently and then practice them again and again.

As per the CBSE Class 9 Syllabus of Maths, there are a total of 6 units, namely- Number System, Algebra, Coordinate Geometry, Geometry, Mensuration, and Statistics. Students are recommended to go through the whole syllabus to familiarize themselves with the concepts and topics included in it.

Class 9 Maths Syllabus 2025-26 Marks Distribution

For the current academic year, the CBSE Class 9 Maths syllabus is essentially the same as it was last year. Notably, there are also no notable changes to the examination pattern. The total marks allotted for the Class 9 Maths Exam is 100 Marks, which is divided into two:

  • Theory/Written Exam: 80 Marks
  • INTERNAL ASSESSMENT- 20 Marks

Let’s take a quick tour of the unit-wise marks distribution of the CBSE Class 9 Maths Syllabus in the table below.

S. No. Name of Unit Marks
1 NUMBER SYSTEMS 10
2 ALGEBRA 20
3 COORDINATE GEOMETRY 4
4 GEOMETRY 27
5 MENSURATION 13
6 STATISTICS & PROBABILITY 6
TOTAL 80

CBSE Class 9 Maths Syllabus 2025-26 Unit Wise

The Class 9 Mathematics Syllabus is divided into six units, and each unit discusses a unique concept of the Mathematical Operations. Here we have shared a list of topics and subtopics included in the CBSE Class 9 Maths Syllabus 2026.

UNIT I: NUMBER SYSTEMS

UNIT I: NUMBER SYSTEMS
1. REAL NUMBERS
  1.  Review of representation of natural numbers, integers, and rational numbers on the number line. Rational numbers as recurring/ terminating decimals. Operations on real numbers.
  2.  Examples of non-recurring/non-terminating decimals. Existence of non-rational numbers (irrational numbers) such as , and their representation on the number line. Explaining that every real number is represented by a unique point on the number line and conversely, viz. every point on the number line represents a unique real number.
  3. Definition of nth root of a real number.
  4. Rationalization (with precise meaning) of real numbers of the type 1/(a+b√x) and 1/(√x+√y) (and their combinations) where x and y are natural number and a and b are integers.
  5. Recall of laws of exponents with integral powers. Rational exponents with positive real bases (to be done by particular cases, allowing learner to arrive at the general laws.)

UNIT II: ALGEBRA

Unit II: ALGEBRA
1. POLYNOMIALS
  • Definition of a polynomial in one variable, with examples and counter examples. Coefficients of a polynomial, terms of a polynomial and zero polynomial. Degree of a polynomial. Constant, linear, quadratic and cubic polynomials. Monomials, binomials, trinomials. Factors and multiples. Zeros of a polynomial. Motivate and State the Remainder Theorem with examples.
  • Statement and proof of the Factor Theorem. Factorization of ax²+ bx + c, a ≠ 0 where a, b and c are real numbers, and of cubic polynomials using the Factor Theorem.
  • Recall of algebraic expressions and identities. Verification of identities and their use in factorization of polynomials.

1
2. LINEAR EQUATIONS IN TWO VARIABLES Recall of linear equations in one variable. Introduction to the equation in two variables. Focus on linear equations of the type ax + by + c=0.Explain that a linear equation in two variables has infinitely many solutions and justify their being written as ordered pairs of real numbers, plotting them and showing that they lie on a line.

UNIT III: COORDINATE GEOMETRY

UNIT III: COORDINATE GEOMETRY
COORDINATE GEOMETRY The Cartesian plane, coordinates of a point, names and terms associated with the
coordinate plane, notations.

 

UNIT IV: GEOMETRY

UNIT IV: GEOMETRY
1. INTRODUCTION TO EUCLID’S GEOMETRY History – Geometry in India and Euclid’s geometry. Euclid’s method of formalizing observed phenomenon into rigorous Mathematics with definitions, common/obvious notions, axioms/postulates and theorems. The five postulates of Euclid. Showing the relationship between axiom and theorem, for example:

  • (Axiom) 1. Given two distinct points, there exists one and only one line through them.
  • (Theorem) 2. (Prove) Two distinct lines cannot have more than one point in common.
2. LINES AND ANGLES
  1. (Motivate) If a ray stands on a line, then the sum of the two adjacent angles so formed is 180º and the converse.
  2. (Prove) If two lines intersect, vertically opposite angles are equal.
  3. (Motivate) Lines which are parallel to a given line are parallel.
3.TRIANGLES
  1. (Motivate) Two triangles are congruent if any two sides and the included angle of one triangle is equal to any two sides and the included angle of the other triangle (SAS Congruence).
  2. (Prove) Two triangles are congruent if any two angles and the included side of one triangle is equal to any two angles and the included side of the other triangle (ASA Congruence).
  3. (Motivate) Two triangles are congruent if the three sides of one triangle are equal to three sides of the other triangle (SSS Congruence).
  4. (Motivate) Two right triangles are congruent if the hypotenuse and a side of one triangle are equal (respectively) to the hypotenuse and a side of the other triangle. (RHS Congruence)
  5. (Prove) The angles opposite to equal sides of a triangle are equal.
  6. (Motivate) The sides opposite to equal angles of a triangle are equal.
4. QUADRILATERALS
  1. (Prove) The diagonal divides a parallelogram into two congruent triangles.
  2. (Motivate) In a parallelogram opposite sides are equal, and conversely.
  3.  (Motivate) In a parallelogram opposite angles are equal, and conversely.
  4. (Motivate) A quadrilateral is a parallelogram if a pair of its opposite sides is parallel and equal.
  5.  (Motivate) In a parallelogram, the diagonals bisect each other and conversely.
  6. (Motivate) In a triangle, the line segment joining the mid points of any two sides is parallel to the third side and in half of it and (motivate) its converse.
5. CIRCLES
  1. (Prove) Equal chords of a circle subtend equal angles at the center and (motivate) its converse.
  2. (Motivate) The perpendicular from the center of a circle to a chord bisects the chord and conversely, the line drawn through the center of a circle to bisect a chord is perpendicular to the chord.
  3. (Motivate) Equal chords of a circle (or of congruent circles) are equidistant from the center (or their respective centers) and conversely.
  4. (Prove) The angle subtended by an arc at the center is double the angle subtended by it at any
    point on the remaining part of the circle.
  5. (Motivate) Angles in the same segment of a circle are equal.
  6. (Motivate) If a line segment joining two points subtends equal angle at two other points lying
    on the same side of the line containing the segment, the four points lie on a circle.
  7. (Motivate) The sum of either of the pair of the opposite angles of a cyclic quadrilateral is 180°
    and its converse.

UNIT V: MENSURATION

UNIT V: MENSURATION
1. AREAS Area of a triangle using Heron’s formula (without proof)
2. SURFACE AREAS AND VOLUMES Surface areas and volumes of spheres (including hemispheres) and right circular cones.

 

UNIT VI: STATISTICS

UNIT VI: STATISTICS
STATISTICS Bar graphs, histograms (with varying base lengths), and frequency polygons

 

CBSE Class 9 Maths Syllabus 2025-26 PDF Download

The Central Board of Secondary Education has released an official CBSE Class 9 Maths Syllabus 2025-26 PDF on its official website at cbseacademic.nic.in. Apart from the syllabus, it contains crucial details like the marking scheme, exam pattern, unit-wise breakdown, and so on. To get more details, download the Class 9 Syllabus PDF by clicking the direct link given below.

Maths_Sec_2025-26 PDF

CBSE Class 9 Maths Syllabus 2026: FAQs

1. What is the CBSE Class 9 Maths syllabus for 2026?

The Class 9 Mathematics syllabus follows the NCERT/CBSE curriculum and includes six major units:

  1. Number Systems

  2. Algebra

  3. Coordinate Geometry

  4. Geometry

  5. Mensuration

  6. Statistics
    (Source: CBSE syllabus references & educational sites)

Each unit comprises important chapters and concepts students must learn for the annual exam.

2. How many units and marks are there in the syllabus?

The syllabus is divided into six units with the following theory marks distribution:

Unit Name Marks
I Number Systems 10
II Algebra 20
III Coordinate Geometry 4
IV Geometry 27
V Mensuration 13
VI Statistics 6
Total (Theory) — 80

Internal assessment (not shown above) contributes 20 marks, making the overall evaluation out of 100.

3. What are the main topics under each unit?

Number Systems
• Real numbers and their decimal expansions (rational/irrational).
• Representation on the number line.
• Operations on real numbers.

Algebra
• Polynomials.
• Linear equations in two variables and their solutions.

Coordinate Geometry
• Cartesian plane and coordinates of points.

Geometry
• Euclid’s geometry fundamentals, lines & angles.
• Triangles and their congruence.
• Quadrilaterals and circles.

Mensuration
• Heron’s formula for the area of a triangle.
• Surface areas and volumes of 3D shapes.

Statistics
• Data representation and basic statistics.

4. Is the syllabus for 2026 different from previous years?

There hasn’t been a major reduction or structural change in the Class 9 syllabus for 2025-26 (which applies to the 2026 annual exams). The units and topics remain consistent with the latest official guidelines.

However, students should check for deleted topics (specific sub-topics removed from NCERT books), as indicated in rationalisation lists, to avoid studying content not evaluated in exams.

5. What is the exam pattern for Class 9 Maths 2026?

The main exam structure (80 marks) includes multiple types of questions:

  • ∼20 MCQs (1 mark each)

  • Short answers (2–3 marks)

  • Long answers (5 marks)

  • Case-based questions (4 marks)

There is internal choice in some questions to help students answer according to comfort.

6. Do I need to study all chapters of NCERT?

Yes, NCERT Class 9 Maths textbook is the primary resource. Focus on conceptual understanding and all exercises, since the exam tests both fundamental and applied knowledge.

Also, check which topics have been deleted or rationalised in the curriculum so you don’t spend time on content not included in the current syllabus.

7. Which chapters are important or high-weightage?

Most units carry significant marks, but traditionally:

  • Algebra and Geometry have the highest weightage.

  • Understanding of Real Numbers, Triangles, and Surface Areas & Volumes is critical for exams.

8. Are there any changes planned in the assessment for Class 9?

CBSE has announced that open-book assessments (OBAs) for Class 9 will be introduced from the 2026-27 academic session (next year), promoting analytical and application-based learning.

This may influence future evaluation formats, but for the 2026 board exams, the traditional format applies.

9. Where can I download the official syllabus PDF?

You can download the official CBSE Class 9 Maths syllabus PDF from the CBSE Academic website under the “Curriculum 2025-26” section.

10. Quick tips for preparation

  • Start with the NCERT textbook and finish all exercises.

  • Practice sample papers based on the exam pattern.

  • Revision of core concepts regularly improves problem-solving speed.

  • Focus on diagrams and proofs in Geometry. (General guidance based on typical CBSE prep norms)

About The Author

0ad1e1aeac0f35aa9ab3e5bf4f7eea59512f01d64edf3eeed05183fd6f852879?s=150&d=mm&r=g

Brajesh

Brajesh (MCA, M.Tech (IT)) is a passionate education and career content creator with a strong academic background in Computer Applications (MCA) and Technology (M.Tech). With years of hands-on experience in exam preparation strategies, syllabus analysis, and government job updates, he helps students and aspirants navigate their academic and professional journeys with clarity and confidence.

See author's posts

Leave a Comment